The product of thinking about computer science problems with every spare moment over a week has left me with a a terrible sense of humor and an undeniable need to make ludicrous analogies, this post is the latter.
The Travelling Salesman Problem or TSP for abbreviation junkies is a well known problem in computer science (or sales). Given a list of cities and locations, one must find the shortest path that visits all cities exactly once. What's up with that exactly once clause? I don't know about you, but I find that to be an awkward restriction for a travelling salesman. You're going to want to loop back and revisit towns you unloaded your wares in earlier unless you're selling miracle elixirs or IPO shares. Shall we rename the travelling salesman, the travelling charlatan?
The complexity of the problem comes into play because the number of potential paths grows as a factorial of the number of cities and paths. Simple heuristics like locally finding the nearest neighbor are easily proven to fail to find the global minimum and may diverge far from the ideal solution.
A different travelling salesman problem
What if the salesman doesn't know where each of the cities are? What if some cities have no interest in buying or become ghost towns before the salesman arrives? What if the salesman needs to make enough sales to cover living expenses at each city? Would you agree that the problem has become even more challenging? Now the salesman has limited reach, and may end up at destinations without eager customers. I thought about this type of problem from a more realistic salesman perspective, as I've had my fill of theory this week. The final piece of the puzzle madness pie came when I thought to replace the salesman with another species, in particular a shark. My inspiration, life finds solution to intractable problems every day.
A shark may find its meals far and few between. If the shark fails to find it's next meal before it's energy runs out, it faces a grim fate. Now we have dynamic locations with available food (4D x,y,z,T), dynamic reach as the shark can swim only so far, and an ongoing motivation to continue searching out meals in order to survive (hunger). I'm curious what genetically coded strategies in the shark's mind enable it to efficiently seek out nourishment, and how may we mimic fragments of those algorithms.
Let's begin the investigation by seeking patterns in how a shark may find its prey. It's known that sharks have an uncanny sense of smell for blood in the water, and this can guide them to find prey over long distances. But what tactics do sharks take when lacking observations?
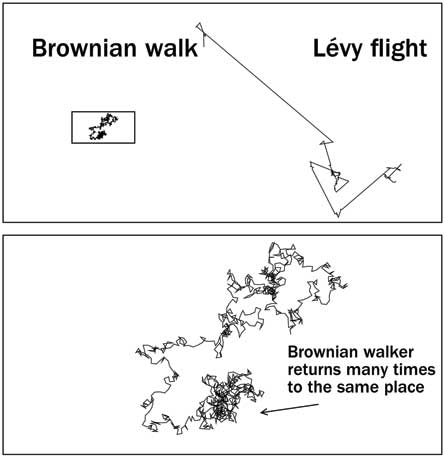
The above image and the following excerpt are from a science news article, "Sharks use math to hunt".
</a>
A new study suggests that some sharks and other marine predators can follow strict mathematical strategies when foraging for dinner. The work, reported online June 9 in Nature, is the latest aiming to show whether animals sometimes move in a pattern called a Lévy walk.
Unlike random motion — in which animals take similar-sized steps in any direction, like a drunk stumbling around — Lévy walks are punctuated by rare, long forays in any direction. Draw a Lévy walk on a graph, and its squiggly pattern echoes a fractal, the mathematical phenomenon whose shape remains similar no matter the viewing scale.
“Living organisms, when allowed to make freely willed decisions, seem to end up obeying some kind of mathematical law,” says Gandhimohan Viswanathan, a theoretical physicist at the Federal University of Alagoas in Maceió, Brazil, who was not involved in the study.
Biologists had long thought that animal foraging was dominated by random walks. But in 1996 a team led by Viswanathan reported that wandering albatrosses, fitted with radio-tracking devices, made the occasional long flight that is the hallmark of a Lévy pattern.
Soon, biologists were reporting Lévy behavior in everything from deer to bumblebees and speculating how it might drive human migrations or the spread of genetically engineered crops. But many of those studies were flawed, says David Sims, a researcher at the Marine Biological Association of the United Kingdom in Plymouth. “Patchy data could mean you think you have a Lévy flight when you haven’t,” he says. And in 2007, researchers debunked the original 1996 albatross paper by noting that many of the reported “Lévy walks” — in which the birds’ transmitters remained dry, supposedly during extended flight — actually were birds resting on their nests.
Now, however, Sims and his colleagues say they have firm evidence for Lévy behavior in 14 species of open-ocean marine predators, including tuna, swordfish, marlin and sharks (although not great whites). The key is the sheer amount of data, on depth and location, gathered by electronic tags, says Sims. His group collected more than 12 million data points describing how the animals swam in the ocean over 5,700 days.
I've mangled the Travelling Salesman Problem, and gone off on a tangent about how sharks statistically roam for food. But there may be a shred of hope in counting on living organisms to solve computationally intractable problems like the TSP. While doing a little leg work early this morning, I came across an intriguing section of the TSP Wikipedia page. Marco Dorigo, outlined a heuristic method of solving the problem by simulating ant colonies (Ant Colony System or ACS). This field of study is called ant colony optimization and it has produced near-optimal solutions to the TSP.
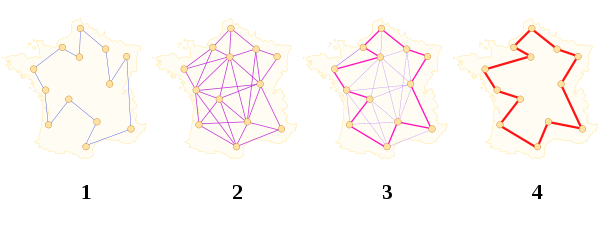
It models behavior observed in real ants to find short paths between food sources and their nest, an emergent behaviour resulting from each ant's preference to follow trail pheromones deposited by other ants.
ACS sends out a large number of virtual ant agents to explore many possible routes on the map. Each ant probabilistically chooses the next city to visit based on a heuristic combining the distance to the city and the amount of virtual pheromone deposited on the edge to the city. The ants explore, depositing pheromone on each edge that they cross, until they have all completed a tour. At this point the ant which completed the shortest tour deposits virtual pheromone along its complete tour route (global trail updating). The amount of pheromone deposited is inversely proportional to the tour length: the shorter the tour, the more it deposits.

