Functions solving linear equations without loops or recursion

In this morning's post I'll touch on a topic I couldn't immediately wrap my head around. I've run into the subject of Lambda calculus before, but ignored it for three reasons.

First because it was usually associated with Scheme and I could never balance parenthesis inducing immediate brain shutdown
Second and more importantly in nearly fifteen years of developing I never required it in practice
And finally even if I did have a need I wouldn't be able to leverage it as a tool in my primary work environment, lambdas and c++ are like oil and water¹

The above rationale has since become null and void due to my near fanatic interest in a number of different programming languages and frameworks. I came across a tutorial this morning which walks through a JavaScript implementation of a fixed point combinator.

Equations and Fixed Points

Let's begin with an equation and see how it's solution is defined by it's fixed points:
x = x² - 2
This example is taken from an
Implementation of fixed point Y Combinator in JavaScript.

Recursion as fixed points

It turns out that students learning algebra are already familiar with recursion and fixed points. They just don’t realize it. Consider an equation like “x = x² - 2.” (Programmers might recognize this as a recursive definition, in which x is being defined in terms of itself.)

If asked to solve for the value of x, a student might re-arrange the equation to use the quadratic formula. However, there is another way to express, and even find, the value(s) of x: fixed points.

A fixed point of a function f is an input that is equal to its output; that is x is a fixed point of the function f if x = f(x). Some functions have no fixed points; some have many. The notation Fix(f) denotes the set of fixed points of a function f.

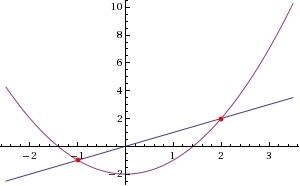
Define the function f such that f(v) = v2 - 2. Then, observe that the original equation may now be re-written as "x = f(x)." In other words, the solutions to the equation are the fixed points of the function f! That is, Fix(f) = {-1,2}--a fact we can verify by seeing that

f(-1) = (-1)² - 2 = 1 - 2 = -1,
and:
f(2) = (2)² - 2 = 4 - 2 = 2
or by graphing y = x and y = f(x):

These are exactly the solutions to x = x² - 2 given by Wolfram Alpha.

The insight that powers the upcoming technique is the observation that any time we have a recursive definition of the form “x = f(x),” the meaning of x is going to be defined in terms of fixed points. The trick is to find a way to obtain fixed points when the equation has the form “f = F(f),” in which the value of f is not a number, but an actual function. The Y combinator is that trick.

The Y combinator in theory

In his research on the λ-calculus and combinatory logic, Haskell Curry discovered the “paradoxical” fixed-point combinator known as the Y combinator. The Y combinator takes a functional as input, and it returns the (unique) fixed point of that functional as its output. A functional is a function that takes a function for its input. Therefore, the fixed point of a functional is going to be a function.

Using the concepts of functionals and fixed points, we can eliminate explicit recursion for a function through two steps:

Find a functional whose fixed point is the recursive function we seek.

Find the fixed point of a functional without recursion.

A simple source transformation takes care of the first step. The Y combinator takes care of the second.
Background:

Lambda:
λv.e == function (v) { return e ; }

Y(F) = F(Y(F))
function Y(F) {
    return F(Y(F)) ;
}

Y(F) = F(λ x.(Y(F))(x))

function Y(F) {
    return F(function (x) {
        return (Y(F))(x) ;
    });
}


http://www.ucombinator.org/, recursive dependency on Y removed
Y = (λh.λF.F(λ x.((h(h))(F))(x))) (λh.λF.F(λ x.((h(h))(F))(x)))

The code below is executable in javascript

// A "functional" is just a function that takes
// another function as input.  
// The Y combinator finds the fixed point
// of the "functional" passed in as an argument.
// Thus, the Y combinator satisfies the property:
//     Y(F) = F(Y(F))
// Note that Y does not reference itself:

var Y = function(F) {
    return (function(x) {
        return F(function(y) {
            return (x(x))(y);
        });
    })(function(x) {
        return F(function(y) {
            return (x(x))(y);
        });
    });
};

// (In fact, all functions above are anonymous!)
// FactGen is the functional whose fixed point is
// factorial.
// That is, if you pass the factorial function to
// FactGen, you get back the factorial function.
// Since the Y combinator returns the fixed point
// of a functional, applying the Y combinator to
// FactGen returns the factorial function!
// Note that FactGen does not reference itself:

var FactGen = function(fact) {
    return (function(n) {
        return ((n === 0) ? 1 : (n * fact(n - 1)));
    });
};


document.getElementById("result2").innerHTML =
    (Y(FactGen))(6);

What is a Y Combinator?

Mike Vanier's post is the top rated answer from every coder's ally StackOverflow, and his lengthy post is a self proclaimed expansion of chapter 9 from
the Little Schemer.

What the Y combinator is and what it does

The Y combinator is a higher-order function. It takes a single argument, which is a function that isn't recursive. It returns a version of the function which is recursive. We will walk through this process of generating recursive functions from non-recursive ones using Y in great detail below, but that's the basic idea.
More generally, Y gives us a way to get recursion in a programming language that supports first-class functions but that doesn't have recursion built in to it. So what Y shows us is that such a language already allows us to define recursive functions, even though the language definition itself says nothing about recursion. This is a Beautiful Thing: it shows us that functional programming alone can allow us to do things that we would never expect to be able to do (and it's not the only example of this).

In the section following this quote Mike defines and describes related topics sucks as Lazy Evaluation, Combinators, functions as data, etc.

This post is something I'll refer back to as I'll need at least a few rereads of the linked examples, and time to get my hands dirty with with the code before I feel more comfortable with the topic. At this point I'm a little confused, but the lambda calculus that's used to remove the recursive dependency appears to bear similarity to algebraic manipulation before factoring in mathematics.

Other Y Combinator Implementations:

Y Combinator in Ruby Autovivification

Deriving the Y Combinator (JavaScript)

Y Combinator in Python

Notes:

C++ was my dominant programming environment up until two years ago. Learning, using, and thinking in a variety of other languages has opened my world to the natural beauty of code

Victus Spiritus