"The difference between a bad programmer and a good one is whether he considers his code or his data structures more important. Bad programmers worry about the code. Good programmers worry about data structures and their relationships"
Linus Torvalds
</blockquote>
In this third chapter overviewing computer science the thrill ride continues. I'll peak into the mind of madness, and give form to the chaos of raw information. Structured data empowers developers to move beyond the troublesome issues of I/O and manipulation, and frees their minds to consider the flow of data between well understood containers.

- Intro and Big O
- Object Oriented Programming
- Data Structures: arrays, lists, trees, hash tables
- Algorithms (searches, sorts, maths!)
- Graphs, Networks, and Operating Systems
Basic Variable Types or Primitives
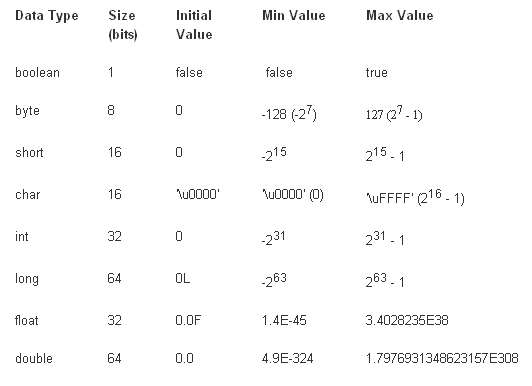
Primitives are basic building blocks which have known size and known persistence (just beware of endianess or the byte order). The primitive types are similar between java and c/c++ and include: simple 8 bit/1 byte chars, booleans (usually 1 byte), 2 byte shorts, 4 byte integers (and pointers in c/c++), 8 byte long integers (long longs in c++), 4 floating point (IEEE), and 8 byte double precision floating point types. The collection of these primitive types allow optimized execution balanced with storage size.
Collections (not the repo man)

The trade offs between choices of data structures are based on space, search, insertion and deletion times. I'll mention big O values for a selection of operations but I don't have a full table of those handy (if you know of a great image/table please let me know).
- Arrays: Arrays are collections of elements accessed by an index. They are generally implemented with a contiguous block of memory. Access time of a known index is O(1), search is O(n), search of an ordered array O(log n). Insertion and deletion mid array can be expensive.
- Linked Lists: are a sequence of nodes which contain an element and a link to the next node. Access time usually requires walking the list and is O(n). Various forms of lists exist including but not limited to circular (end node points to first node), singly (single link element per node), doubly (links forward and backward), and multiply (links to more than 2 nodes) linked lists.
- Hash, Lookup Table, Map, or Associative Array: Instead of using an index like a basic array, Hashes use a key to lookup elements. Lookups, insertion and deletion are O(1) when using hash tables in memory (the table maps the key to an index). Maps have O(logn) lookups and insertions.
- Tree: Trees can be thought of as multi-branch structures which begin at a root node and extend to reach all nodes. Self balancing binary trees are one of the implementations used to provide hash lookup tables above. When Hashes grow beyond memory B-trees are used. Balanced binary trees have O(log n) for search, insert or deletion.
Examples of Data Structures

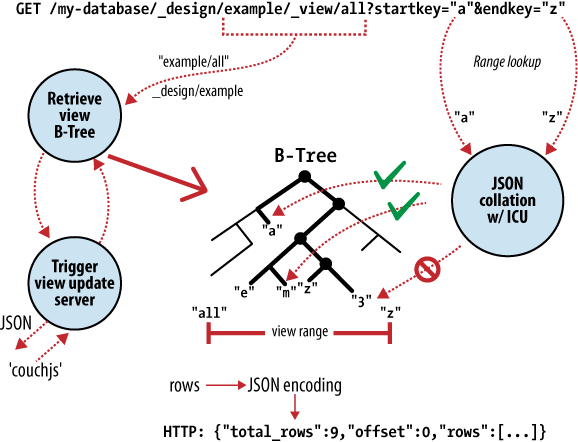
Case Study: CouchDB BTree Storage
Internal storage is JSON data in a B-Tree structure. This framework enables O(log N) speed lookups, insertions and deletions. The following diagram, from the definitive guide eventual consistency section, shows how a view request is handled:
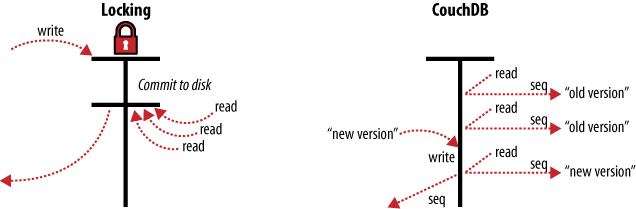
An important restriction that feeds directly into CouchDB's ability to scale, documents are accessible only by key, and rely on multi-version concurrency control to manage concurrent access (no locking).
STL and Boost Data Structures
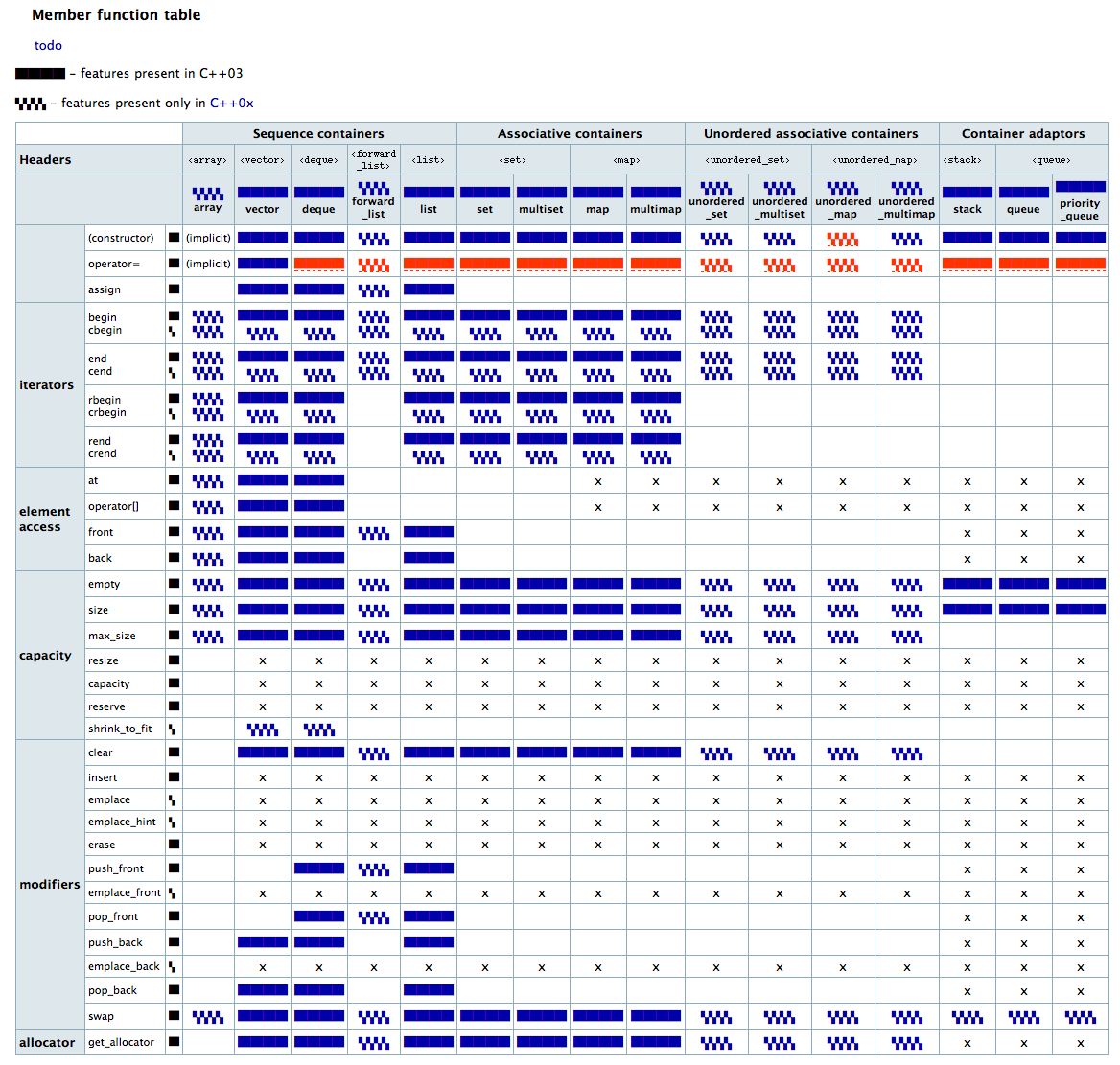
STL and Boost are libraries which support many advanced data types for c++. Before STL was heavily adopted as a standard, my coworkers and I developed our own basic data structures (arrays, lists, vectors, matrices, etc) using templates. The good news is, they're much easier to step into when something goes wrong :).
- STL documentation (my colleagues in Tucson pointed me here)
- Boost documentation
- Great answer on big O for a handful of STL containers
Red Black Tree (sorted has interface in Ruby)
The Ruby implementation of the RBTree is a sorted associative collection.
RBTree is a sorted associative collection that is implemented with Red-Black Tree. The elements of RBTree are ordered and its interface is the almost same as Hash, so simply you can consider RBTree sorted Hash.
Red-Black Tree is a kind of binary tree that automatically balances by itself when a node is inserted or deleted. Thus the complexity for insert, search and delete is O(log N) in expected and worst case. On the other hand the complexity of Hash is O(1). Because Hash is unordered the data structure is more effective than Red-Black Tree as an associative collection.